

The Butterfly Problem
by
Ana Kuzle
Problem:
Through the midpoint M of any chord PQ of a circle, any chords AB and CD are drawn; lines AD and BC meet PQ at points X and Y. You many want to construct a line PQ containing the chord PQ. Prove that M is the midpoint of XY. Constructing a valid picture of this situation is a part of the problem, but only the first step in building the proof. Be sure that your constructions illustrate the possibilities where X and Y can be either inside the circle or outside of it.
With line PQ, construct lines AC and BD. If AC and BD are the intersections points X and Y with line PQ, what can you prove about the relationship of M, X, and Y.
| This problem is known as the Butterfly problem. You can see in the picture that the shape that triangles AMD,and CMD make looks like a butterfly. | |
 |
By measuring using GSP I got that M is the midpoint of the segment XY. Attached you can find a gsp file with animation of both cords AB, and CD. As they move along the circumference, point M remains the midpoint of the segment XY.
Statement: M is the midpoint of the segment XY.
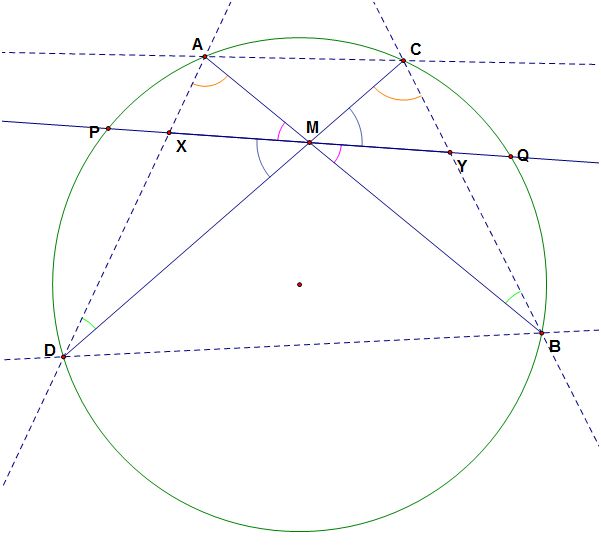 |
Let us look at two triangles, triangle AMD, and triangle CMB. From the construction we can see that <DAB=<DCB, and <ADC=<ABC because these are angles subtending equal arcs, DB, and AC respectively. Also, <AMD=<CMB because they are vertical angles. Thus, according to AAA postulate triangles ADM, and CBM are similar. Hence, AM/CM=DM/BM. If we multiply this by CM·BM, we get that AM·BM=CM·DM. This result is commonly known as the power of a point theorem. Furthermore, <AMX=<BMY, and <XMD=<YMC because they are vertical angles. Let us now look at the triangles APX, and QDX. For the same reasons as above (AA postulate),triangles APX and QDX are similar (<AXP=<QXD because they are vertical angles, and <XDQ=<APX because they subtend equal arc AQ). Using the power point theorem we get that AX·DX=PX·QX. Also, using the same reasoning we get that triangles CQY and MPY are similar, and CY·BY=QY·PY. Reader can easily see from the picture which angles are congruent because they are in the same color. |
Let us denote PM=a, and MX=x. Similarly, let QM=b, and MY=y. But from the premises of the problem we know that PM=QM, so PM=QM=a.
From AX·DX=PX·QX, we get that AX·DX=(PM-MX)·(QM+MX)=(a-x)(a+x)=a^2-x^2. Thus, we have AX·DX=a^2-x^2. (6)
Similarly, CY·BY=QY·PY. Again, CY·BY=(MQ-MY)·(PM+MY)=(a-y)(a+y)=a^2-y^2. (7)
Let us have in mind that we want to prove that x=y, i.e. MX=MY. Thus, by looking at (6), and (7) I got an idea that if I could prove something like AX·DX=CY·BY, or k·MX^2/l·MY^2=(AX·DX)/(CY·BY) and k=l (5), the initial statement would be proven.
Since we have product of triangle segments, let us look at the areas of triangles. Using conclusions about congruence of certain angles and formulas for the area of the triangle we have the following:
Taking a closer look at the left side we can see that the area of the same triangle is expressed twice but in a different way. Thus, we can multiply (1), and (2) by the inverse of (3), and (4). In this way we get 1 on the left side. Multiplying all those expressions we get,
Hence, this is what we wanted to get as said in (5). From (6), and (7) we have
(8)
From (8) we get,
(9)
Since, a is the length, it is not equal to zero so we can divide (9) by a. Therefore, . Taking a square root, and having in mind that both x, and y are also lengths (positive numbers) we get that x=y.
If we go back, we can see that we denoted x=MX, and y=MY. Thus, MX=MY.
From the definition of a midpoint as a point equidistant from its end points we have proven our statement. Thus, M is the midpoint of the segment XY.
Q.E.D.